2009
11.02
11.02
The function defined by
where
, and the exponent
is any real number, is called an exponential function with base
When you work with exponential functions, it may be necessary to apply rules for exponents. These rules are as follows, where and
are real numbers and
and
are positive.
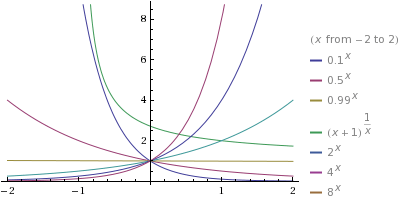
Graphs of some exponential functions are shown below:
Here, some properties of exponential functions
- The domain of an exponential function is all real numbers
- The range is all positive real numbers
- Since
for every base
, each graph has y-intercept (0, 1). There is no x-intercept.
- If
, then
is an increasing function; its graph rises from left to right. Also
and
- Thus as
, the graph has the x-axis as a horizontal asymptote.
- If
, then
is a decreasing function; its graph falls from left to right. Also
and
- Thus as
, the graph has the x-axis as the horizontal asymptote.
No Comment.
Add Your Comment