The limit of as approaches is the number , written

provided the is arbitrarily close to for all sufficiently close to, but not equal to, . A Limit is independent of the way (from the left or from the right) in which approaches . Here are some properties of limits:

• 
• 
• 
• 
• 
• *

* If is even, must be positive

Tip! Wolfram Alpha makes calculating limits really easy. Check this out.

Many people, including myself, might not like editing .r (source) files in R itself. Therefore I present you a very ingenious way of avoiding this.

“NppToR provides R language syntax highlighting, code folding, and auto-completion to Notepad++. In addition, it provides Rgui style code passing between Notepad++ and the Rgui.”

To use NppToR the first step is to download and install R. Secondly, we dowload and install notepad++. Finally, we download and install NppToR.

Open NppToR by clicking on . In the settings window we can see/edit which hot-keys to use and adjust a few thing.

An .r file in notepadd++ now look like

nppToR Code Snippet (Series Problem)

Passing it to R ( F8 (lines), ^F8 (file) ) results in the following

nppToR code passing

My friend Alexander, pointed out that writing R code is even easier (and more fancy) when editing in Komodo (in combination with SciViews-K). I may come back to that later!

When using the “Stop removing the <p> and <br /> tags when saving and show them in the HTML editor” switch with tinyMCE Advanced in WordPress you finally have newlines! The only problem is that they become huge and thereby really ugly. One way, I found, to overcome this problem is to style br.spacer_

To do this, you have to put:

br.spacer_ {
	line-height: 0;
}

in your theme’s css file. You can find this css file in wp-content/themes/####/

Note that after upgrading your theme you have to do this trick again…

The graph of the quadratic function is parabola.

• If , the parabola opens upwards. If , it opens downwards
• The vertex is
• The y-interacept =
• The x-intercepts are obtained by setting and solving for

This relationship between the value inside the square root (the discriminant), the type of solutions (two different solutions, one repeated solution, or no real solutions), and the number of x-intercepts (on the corresponding graph) of the quadratic is summarized in this table:

a positive number inside the square root	zero inside the square root	a negative number inside the square root
two real solutions	one (repeated) real solution	two complex solutions
two distinct x-intercepts	one (repeated) x-intercept	no x-intercepts

References:

• The Quadratic Formula Explained

A function is a rule that assigns to each input number exactly one output number. The set of input numbers to which the rule applies is called the domain of the function. The set of all output numbers is called the range.

A variable that represents input numbers for a function is called an independent variable. A variable that represents output numbers is called a dependent variable.

Output numbers such as are called function values; they are in the range of .

Lets be specific about the domain of a function. Unless otherwise stated, the domain consists of all real numbers for which the equation makes sense and gives function values that are real numbers.

Hint,

• We cannot divide by zero
• where does not give a real number (imaginary number)

Types of functions

Any function in the form , where is a constant, is called a constant function.

A constant function belongs to a broader class of functions, called polynomial functions. in general a function of the form The number is called the degree of a function, and is the leading coefficient. Note that a nonzero constant function, such as [which can be written as ], is a polynomial function of degree 0.

A function that is the quotient of polynomial functions is called a rational function.

Sometimes more than one equation is needed to define a function.

This is called a compound function.

The function is called the absolute function. Recall that that the absolute value, of a real number is denoted and is defined by,

Graphs

The graph of a function is simply the graph of the function . It consists of all points .

In general, the domain consists of all x-values that are included in the graph, and the range is all y-values that are included.

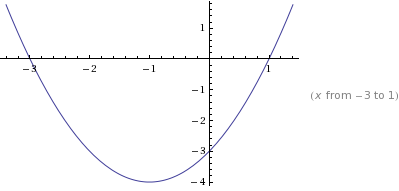
f(x) = x^2 + 2x + 3

It is clear that the domain of this function is all real numbers and the range is all reals

The product is abbreviated where . The letter is called the exponent and the letter is called the base.

The principal nth root of is that the th root of which is if positive if is positive, and is negtive if is negative and is odd.

Thus,

The symbol is called a radical. Here is the index, is the radicand and is the radical sign. With principal square roots we usually omit the index and write instead of .

If the timezone is not set or is wrong, you can run tzconfig to configure it after the operating system is installed. tzconfig will ask you a few simple questions and after that the time will be correct (again).

Your default time zone is set to 'Europe/Amsterdam'.
Local time is now: Wed Oct 28 11:41:01 CET 2009.
Universal Time is now: Wed Oct 28 10:41:01 UTC 2009.

After doing some math assignment for my study I’d really like to publish these things (in wordpress). I found a few ways to do so. One of them was wpmathpub, but I’d rather use LaTeX. Therefore I choose WP LaTeX and because I like it the non easy way I used my server’s installation of LaTeX. A requirement for this is that you have a running LaTeX installation. No problem I thought. Unfortunately, apt was giving me all sorts of errors related to this bug? Fortunately, I found a solution!

First we have to add an apt repositoy

nano /etc/apt/sources.list.d/texlive.list

and add the following lines:

deb http://people.debian.org/~preining/TeX/ tl2007/
deb http://people.debian.org/~preining/TeX/ context/
deb http://people.debian.org/~preining/TeX/ lmodern/
deb http://www.backports.org/debian etch-backports main

Then, we update apt and install the needed packages:

apt-get update

apt-get -t etch-backports install \
	texlive texlive-base texlive-base-bin \
	texlive-context texlive-fonts-recommended texlive-latex-base \
	texlive-latex-recommended texlive-metapost \
	texlive-pdfetex texlive-math-extra

apt-get install install dvipng

If you want to get rid of the warning of your apt-get/aptitude, import this public key into the apt keyring by calling:

wget -qO - http://www.logic.at/people/preining/dsa.asc | apt-key add -

References:

1. TeX Live and Debian

First we have to download osTicket and make it a available via http:

cd /var/www
wget http://osticket.com/dl/osticket_1.6.rc5.tar.gz
tar -xzvf osticket_1.6.rc5.tar.gz
ln -s /var/www/osticket_1.6.rc5/upload /var/www/html/osticket

Then we create a database by means of the MySQL client:

mysql>

CREATE USER 'osticket'@'localhost' IDENTIFIED BY '****************';

GRANT USAGE ON * . * TO 'osticket'@'localhost' IDENTIFIED BY '****************'
	WITH MAX_QUERIES_PER_HOUR 0 MAX_CONNECTIONS_PER_HOUR 0
	MAX_UPDATES_PER_HOUR 0 MAX_USER_CONNECTIONS 0 ;

CREATE DATABASE IF NOT EXISTS `osticket` ;

GRANT ALL PRIVILEGES ON `osticket` . * TO 'osticket'@'localhost';

FLUSH PRIVILEGES;

Change the owner of the osticket folder,

cd /var/www
chown -R apache:apache osticket_1.6.rc5

because include/settings.php must be writable for the installer (user: apache).

Access the installer through http://192.168.1.1/osticket and fill in the right data (e.g. MySQL username and password)

Finally, follow the suggestions of the installer:

• Change permission of include/settings.php to remove write access
• Delete or move setup directory

cd /var/www
chown -R root:root osticket_1.6.rc5
cd osticket_1.6.rc5
mv setup _setup

Optional (for password encryption):

yum install php-mcrypt

Download the latest OTRS package:

wget http://ftp.otrs.org/pub/otrs/RPMS/fedora/4/otrs-2.4.5-01.noarch.rpm

Install it!

rpm -ivh otrs-2.4.5-01.noarch.rpm
error: Failed dependencies:
	perl-DBD-MySQL is needed by otrs-2.4.5-01.noarch
	mysql-server is needed by otrs-2.4.5-01.noarch

You’ll probably get an error.

Install the dependencies and (re)install the OTRS package:

yum install mysql-server
rpm -ivh otrs-2.4.5-01.noarch.rpm

Restart your webserver (apache):

service httpd restart

Use the MySQL client,

mysql>

to execute the following queries (creating a new user + database, and granting all privileges to that database):

CREATE USER 'otrs'@'localhost' IDENTIFIED BY '****************';

GRANT USAGE ON * . * TO 'otrs'@'localhost' IDENTIFIED BY '****************'
	WITH MAX_QUERIES_PER_HOUR 0 MAX_CONNECTIONS_PER_HOUR 0
	MAX_UPDATES_PER_HOUR 0 MAX_USER_CONNECTIONS 0 ;

CREATE DATABASE IF NOT EXISTS `otrs` ;

GRANT ALL PRIVILEGES ON `otrs` . * TO 'otrs'@'localhost';

FLUSH PRIVILEGES;

Then, follow the installer and you should have a working OTRS instance soon…